John Cook: Estimating the exponent of discrete power law data

Suppose you have data from a discrete power law with exponent α. That is, the probability of an outcome n is proportional to n^-α. How can you recover α?

A naive approach would be to gloss over the fact that you have discrete data and use the MLE (maximum likelihood estimator) for continuous data. That does a very poor job [1]. The discrete case needs its own estimator.

To illustrate this, we start by generating 5,000 samples from a discrete power law with exponent 3.

   import numpy.random

   alpha = 3
   n = 5000
   x = numpy.random.zipf(alpha, n)

The continuous MLE is very simple to implement:

    alpha_hat = 1 + n / sum(log(x))

Unfortunately, it gives an estimate of 6.87 for alpha, though we know it should be around 3.

The MLE for the discrete power law distribution satisfies

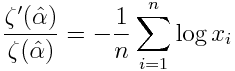
Here ζ is the Riemann zeta function, and x_i are the samples. Note that the left size of the equation is the derivative of log ζ, or what is sometimes called the logarithmic derivative.

There are three minor obstacles to finding the estimator using Python. First, SciPy doesn’t implement the Riemann zeta function ζ(x) per se. It implements a generalization, the Hurwitz zeta function, ζ(x, q). Here we just need to set q to 1 to get the Riemann zeta function.

Second, SciPy doesn’t implement the derivative of zeta. We don’t need much accuracy, so it’s easy enough to implement our own. See an earlier post for an explanation of the implementation below.

Finally, we don’t have an explicit equation for our estimator. But we can easily solve for it using the bisection algorithm. (Bisect is slow but reliable. We’re not in a hurry, so we might as use something reliable.)

    from scipy import log
    from scipy.special import zeta
    from scipy.optimize import bisect 

    xmin = 1

    def log_zeta(x):
        return log(zeta(x))

    def log_deriv_zeta(x):
        h = 1e-5
        return (log_zeta(x+h) - log_zeta(x-h))/(2*h)

    t = -sum( log(x/xmin) )/n
    def objective(x):
        return log_deriv_zeta(x) - t

    a, b = 1.01, 10
    alpha_hat = bisect(objective, a, b, xtol=1e-6)
    print(alpha_hat)

We have assumed that our data follow a power law immediately from n = 1. In practice, power laws generally fit better after the first few elements. The code above works for the more general case if you set xmin to be the point at which power law behavior kicks in.

The bisection method above searches for a value of the power law exponent between 1.01 and 10, which is somewhat arbitrary. However, power law exponents are very often between 2 and 3 and seldom too far outside that range.

The code gives an estimate of α equal to 2.969, very near the true value of 3, and much better than the naive estimate of 6.87.

Of course in real applications you don’t know the correct result before you begin, so you use something like a confidence interval to give you an idea how much uncertainty remains in your estimate.

The following equation [2] gives a value of σ from a normal approximation to the distribution of our estimator.

So an approximate 95% confidence interval would be the point estimate +/- 2σ.

    from scipy.special import zeta
    from scipy import sqrt

    def zeta_prime(x, xmin=1):
        h = 1e-5
        return (zeta(x+h, xmin) - zeta(x-h, xmin))/(2*h)

    def zeta_double_prime(x, xmin=1):
        h = 1e-5
        return (zeta(x+h, xmin) -2*zeta(x,xmin) + zeta(x-h, xmin))/h**2

    def sigma(n, alpha_hat, xmin=1):
        z = zeta(alpha_hat, xmin)
        temp = zeta_double_prime(alpha_hat, xmin)/z
        temp -= (zeta_prime(alpha_hat, xmin)/z)**2
        return 1/sqrt(n*temp)

    print( sigma(n, alpha_hat) )

Here we use a finite difference approximation for the second derivative of zeta, an extension of the idea used above for the first derivative. We don’t need high accuracy approximations of the derivatives since statistical error will be larger than the approximation error.

In the example above, we have α = 2.969 and σ = 0.0334, so a 95% confidence interval would be [2.902, 3.036].

* * *

[1] Using the continuous MLE with discrete data is not so bad when the minimum output x_min is moderately large. But here, where x_min = 1 it’s terrible.

[2] Equation 3.6 from Power-law distributions in empirical data by Aaron Clauset, Cosma Rohilla Shalzi, and M. E. J. Newman.