Absolute values are commonly used in mathematics, physics, and engineering. Although the school definition of an absolute value might seem straightforward, you can actually look at the concept from many different angles. If you intend to work with absolute values in Python, then you’ve come to the right place.
In this tutorial, you’ll learn how to:
- Implement the absolute value function from scratch
- Use the built-in
abs()function in Python - Calculate the absolute values of numbers
- Call
abs()on NumPy arrays and pandas series - Customize the behavior of
abs()on objects
Don’t worry if your mathematical knowledge of the absolute value function is a little rusty. You’ll begin by refreshing your memory before diving deeper into Python code. That said, feel free to skip the next section and jump right into the nitty-gritty details that follow.
Sample Code:Click here to download the sample code that you’ll use to find absolute values in Python.
Defining the Absolute Value
The absolute value lets you determine the size or magnitude of an object, such as a number or a vector, regardless of its direction. Real numbers can have one of two directions when you ignore zero: they can be either positive or negative. On the other hand, complex numbers and vectors can have many more directions.
Note: When you take the absolute value of a number, you lose information about its sign or, more generally, its direction.
Consider a temperature measurement as an example. If the thermometer reads -12°C, then you can say it’s twelve degrees Celsius below freezing. Notice how you decomposed the temperature in the last sentence into a magnitude, twelve, and a sign. The phrase below freezing means the same as below zero degrees Celsius. The temperature’s size or absolute value is identical to the absolute value of the much warmer +12°C.
Using mathematical notation, you can define the absolute value of 𝑥 as a piecewise function, which behaves differently depending on the range of input values. A common symbol for absolute value consists of two vertical lines:
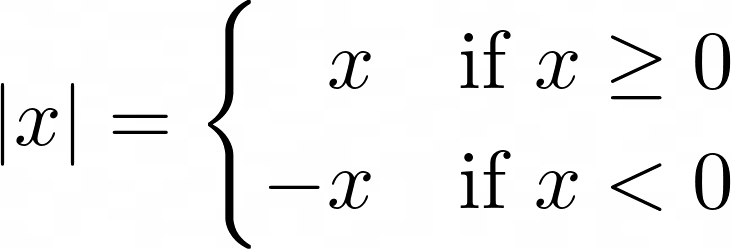 Absolute Value Defined as a Piecewise Function
Absolute Value Defined as a Piecewise Function
This function returns values greater than or equal to zero without alteration. On the other hand, values smaller than zero have their sign flipped from a minus to a plus. Algebraically, this is equivalent to taking the square root of a number squared:
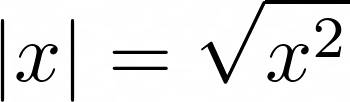 Absolute Value Defined Algebraically
Absolute Value Defined Algebraically
When you square a real number, you always get a positive result, even if the number that you started with was negative. For example, the square of -12 and the square of 12 have the same value, equal to 144. Later, when you compute the square root of 144, you’ll only get 12 without the minus sign.
Geometrically, you can think of an absolute value as the distance from the origin, which is zero on a number line in the case of the temperature reading from before:
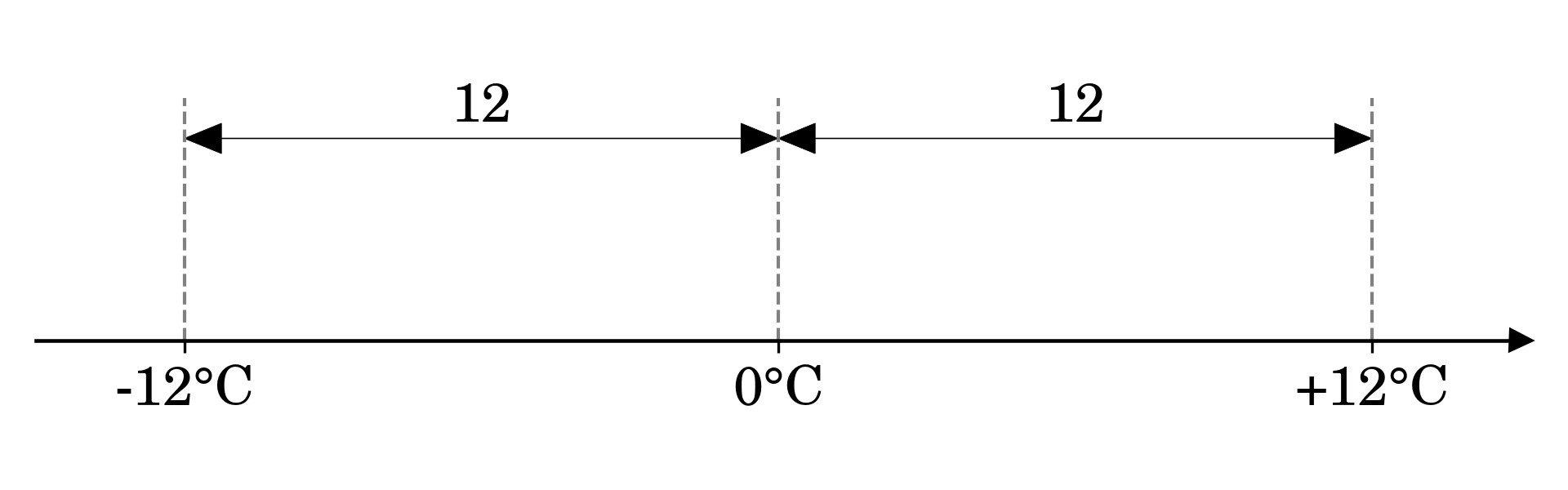 Absolute Value on a Number Line
Absolute Value on a Number Line
To calculate this distance, you can subtract the origin from the temperature reading (-12°C - 0°C = -12°C) or the other way around (0°C - (-12°C) = +12°C), and then drop the sign of the result. Subtracting zero doesn’t make much difference here, but the reference point may sometimes be shifted. That’s the case for vectors bound to a fixed point in space, which becomes their origin.
Vectors, just like numbers, convey information about the direction and the magnitude of a physical quantity, but in more than one dimension. For example, you can express the velocity of a falling snowflake as a three-dimensional vector:
This vector indicates the snowflake’s current position relative to the origin of the coordinate system. It also shows the snowflake’s direction and pace of motion through the space. The longer the vector, the greater the magnitude of the snowflake’s speed. As long as the coordinates of the vector’s initial and terminal points are expressed in meters, calculating its length will get you the snowflake’s speed measured in meters per unit of time.
Note: There are two ways to look at a vector. A bound vector is an ordered pair of fixed points in space, whereas a free vector only tells you about the displacement of the coordinates from point A to point B without revealing their absolute locations. Consider the following code snippet as an example:
>>> A=[1,2,3]>>> B=[3,2,1]>>> bound_vector=[A,B]>>> bound_vector[[1, 2, 3], [3, 2, 1]]>>> free_vector=[b-afora,binzip(A,B)]>>> free_vector[2, 0, -2]A bound vector wraps both points, providing quite a bit of information. In contrast, a free vector only represents the shift from A to B. You can calculate a free vector by subtracting the initial point, A, from the terminal one, B. One way to do so is by iterating over the consecutive pairs of coordinates with a list comprehension.
A free vector is essentially a bound vector translated to the origin of the coordinate system, so it begins at zero.
The length of a vector, also known as its magnitude, is the distance between its initial and terminal points, 𝐴 and 𝐵, which you can calculate using the Euclidean norm:
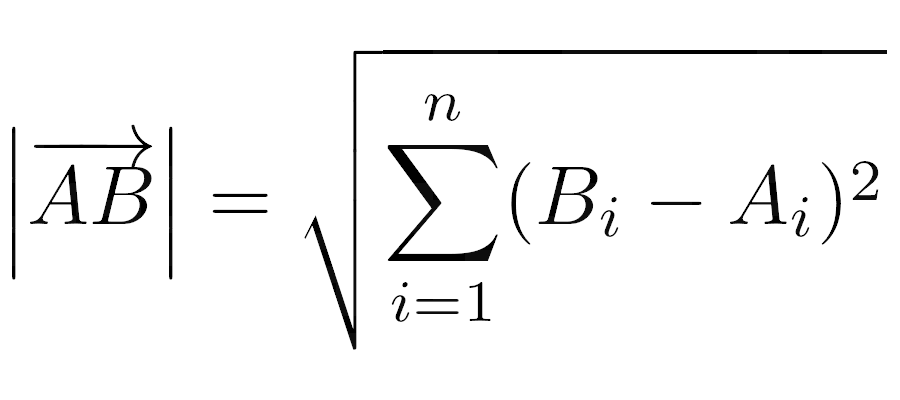 The Length of a Bound Vector as a Euclidean Norm
The Length of a Bound Vector as a Euclidean Norm
This formula calculates the length of the 𝑛-dimensional vector 𝐴𝐵, by summing the squares of the differences between the coordinates of points 𝐴 and 𝐵 in each dimension indexed by 𝑖. For a free vector, the initial point, 𝐴, becomes the origin of the coordinate system—or zero—which simplifies the formula, as you only need to square the coordinates of your vector.
Recall the algebraic definition of an absolute value. For numbers, it was the square root of a number squared. Now, when you add more dimensions to the equation, you end up with the formula for the Euclidean norm, shown above. So, the absolute value of a vector is equivalent to its length!
Read the full article at https://realpython.com/python-absolute-value/ »
[ Improve Your Python With 🐍 Python Tricks 💌 – Get a short & sweet Python Trick delivered to your inbox every couple of days. >> Click here to learn more and see examples ]